计算机图形学GAMES101（十）几何（曲线与曲面）

显示几何

显示几何的表示方法：

1. 点云（Point Cloud）
   不把一个物体的表面用平面来表示，而是用很密集的点来表示。当点足够多时就可以表示一个平面。通常用在扫描中
   
2. 多边形网格（Polygon Mesh）

存储顶点和多边形(通常是三角形或四边形)
更容易处理/模拟
自适应采样更复杂的数据结构
图形中最常见的表示方式

曲线（Curves）

1. ⻉塞尔曲线（Bézier Curves）
   P0为起始点，P3为终止点，P1，P2为控制点，蓝的的线为表示的曲线，该曲线要经过起始点和终止点，但是不要求经过控制点。
   

怎么用任意个数的点画出贝塞尔曲线

德卡斯特里奥算法（de Casteljau Algorithm）

假设起点在时间0，终点在时间1，要画出这条曲线就是要找出时间t=01时，在空间中对于的点的位置。
首先找出t在0到1上的位置（假如时1/3）然后将b0看作0，b1看作1，然后在b0b1找到t对应的位置b0^1^，即1/3处。
同理在b1b2上也找到t相对于的点b1^1^然后将它们连起来。
最后在b0^1^b1^1^上找到t对应的点b0^2^。这就是在t时刻对应空间上的点了。找到时间01上所有的点然后连起来就可以得到曲线了。

多控制点的动态演示：

贝塞尔曲线的代数形式

b0^2^代数形式的求解过程：
可以发现b0^2^(t)=[(1-t)+t]^2^的展开式。

有n个控制点的展开式可以用下面的多项式描述
伯恩斯坦多项式（Bernstein polynomials）：

对于三维空间中的曲线，求曲线上的点可以用下面的式子：

贝塞尔曲线的性质：

• 当t=0时。在起点。t=1时，在终点、即b(0)=b0;b(1)=b3。
• 当控制点为4个时，起始点和终止点的切线分别是b^’^(0)=3(b1-b0);b^’^(1)=3(b3-b2)。
• 想要对一条贝塞尔曲线做仿射变换，只需要对所有控制点做仿射变换然后重新绘制贝塞尔曲线即可。
• 凸包性质：画出来的贝塞尔曲线必需要在控制点形成的凸包内。

凸包：
假设黑色的圈是被拉大的橡皮筋，然后松手，橡皮筋就会收缩到蓝线位置。蓝线所形成的多边形就是这些顶点的凸包。

蓝色的部分是控制点形成的凸包

逐段贝塞尔曲线

因为当控制点过多时，发现贝塞尔曲线并不好控制。
所以采用少量控制点来控制一段曲线，最后把所有曲线都连起来就得到了原本的曲线。

一般采用三次贝塞尔曲线（4个控制点）成为一段。

第一段的终点等于第二段的起点这种连续称作C^0^连续。（相对于函数值相等）

第一段的终点等于第二段的起点，而且切线也要连续（相对于函数一阶导数相等）

曲面

贝塞尔曲面

由4*4个控制点的得到的曲面：

首先对每一列的四个控制点生成一条曲线，然后把得到的四个点又认为是另外一条曲线的控制点，又可以得到一条曲线，该曲线滑动所经过的平面就是贝塞尔曲面。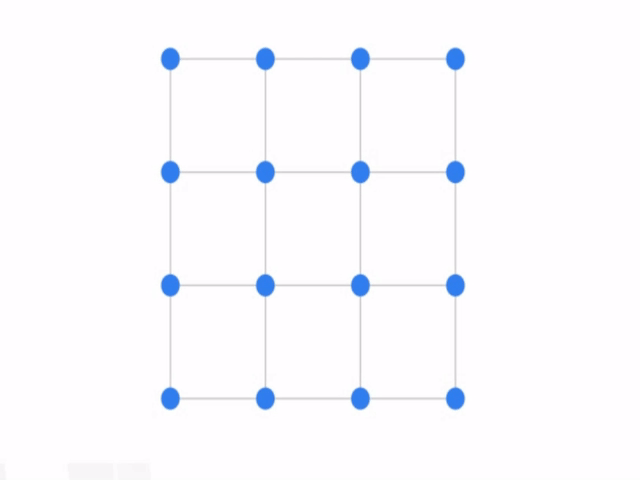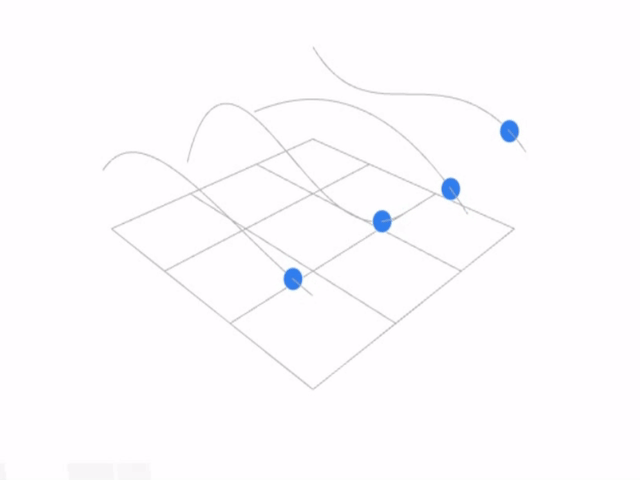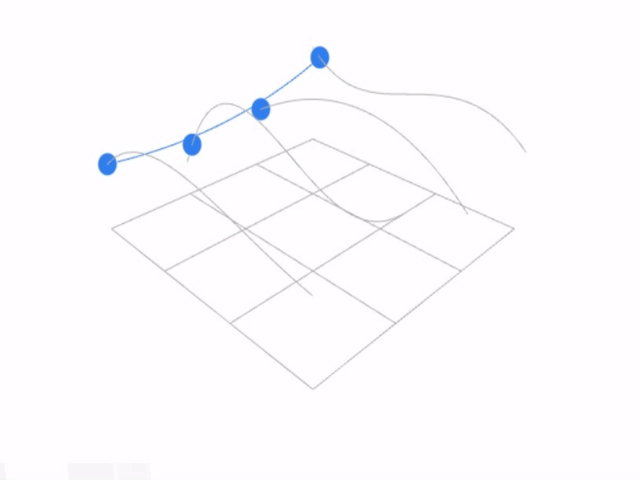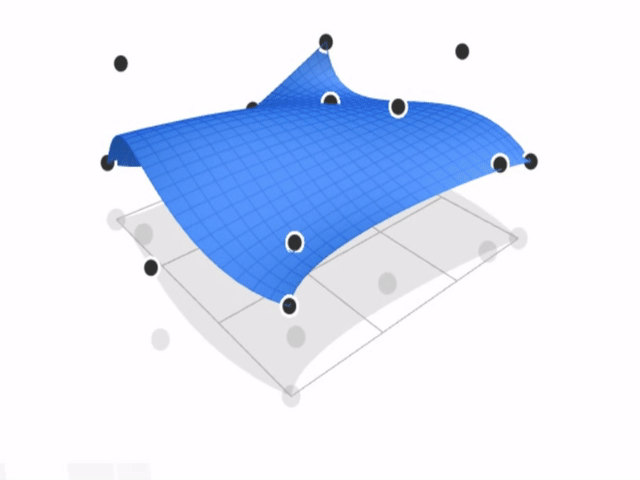

具体流程：

如何找到贝塞尔曲面上的任何一个点：
首先找到四条曲线上时间u的点（对应图片中4个蓝色的点），然后再在蓝色曲线上找时间v所对应的点。所以一个曲面上的点可以用（u，v）来表示。